The eigenvalues can be found by solving the characteristic equation
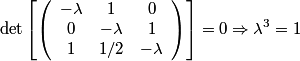 This implies that answer (E) is true. The general solution to 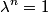 are are 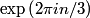 where where 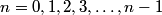 . Therefore, the eigenvalues are . Therefore, the eigenvalues are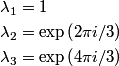 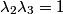 , therefore, answer (C) is also true. , therefore, answer (C) is also true.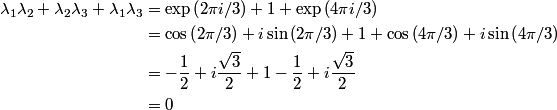 Therefore, answer (D) is also true. 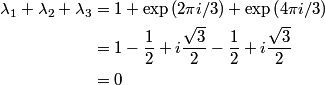 Therefore, answer (A) is also true. Clearly, not all of the roots are real, so answer (C) is correct. |